Understanding both global and layer-specific group structures is useful for uncovering complex patterns in networks with multiple interaction types. In this work, we introduce a new model, the hierarchical multiplex stochastic blockmodel (HMPSBM), that simultaneously detects communities within individual layers of a multiplex network while inferring a global node clustering across the layers. A stochastic blockmodel is assumed in each layer, with probabilities of layer-level group memberships determined by a node's global group assignment. Our model uses a Bayesian framework, employing a probit stick-breaking process to construct node-specific mixing proportions over a set of shared Griffiths-Engen-McCloseky (GEM) distributions. These proportions determine layer-level community assignment, allowing for an unknown and varying number of groups across layers, while incorporating nodal covariate information to inform the global clustering. We propose a scalable variational inference procedure with parallelisable updates for application to large networks. Extensive simulation studies demonstrate our model's ability to accurately recover both global and layer-level clusters in complicated settings, and applications to real data showcase the model's effectiveness in uncovering interesting latent network structure.

Learn more

This paper introduces a periodic multivariate Poisson autoregression with potentially infinite memory, with a special focus on the network setting. Using contraction techniques, we study the stability of such a process and provide upper bounds on how fast it reaches the periodically stationary regime. We then propose a computationally efficient Markov approximation using the properties of the exponential function and a density result. Furthermore, we prove the strong consistency of the maximum likelihood estimator for the Markov approximation and empirically test its robustness in the case of misspecification. Our model is applied to the prediction of weekly Rotavirus cases in Berlin, demonstrating superior performance compared to the existing PNAR model.

Learn more

Understanding the evolving dependence between two sets of multivariate signals is fundamental in neuroscience and other domains where sub-networks in a system interact dynamically over time. Despite the growing interest in multivariate time series analysis, existing methods for between-clusters dependence typically rely on the assumption of stationarity and lack the temporal resolution to capture transient, frequency-specific interactions. To overcome this limitation, we propose scale-specific wavelet canonical coherence (WaveCanCoh), a novel framework that extends canonical coherence analysis to the nonstationary setting by leveraging the multivariate locally stationary wavelet model. The proposed WaveCanCoh enables the estimation of time-varying canonical coherence between clusters, providing interpretable insight into scale-specific time-varying interactions between clusters. Through extensive simulation studies, we demonstrate that WaveCanCoh accurately recovers true coherence structures under both locally stationary and general nonstationary conditions. Application to local field potential (LFP) activity data recorded from the hippocampus reveals distinct dynamic coherence patterns between correct and incorrect memory-guided decisions, illustrating the capacity of the method to detect behaviorally relevant neural coordination. These results highlight WaveCanCoh as a flexible and principled tool for modeling complex cross-group dependencies in nonstationary multivariate systems. Code for implementing WaveCanCoh is available at https://github.com/mhaibo/WaveCanCoh.git.

Learn more

Data collected over networks arise in a number of scientific, engineering and industrial applications, in which the datapoints are noisy observations relating to a process of interest over the graph structure. In this article we propose a novel multiscale representation of data on the edges of a network. In contrast to other methods in the literature which employ expensive node to edge data transformations, our decomposition acts directly on the network edges. Using our method, we propose an efficient edge denoising algorithm, termed E-LOCAAT, which displays good performance across a range of data scenarios, particularly when the number of edges is large. The proposed method is illustrated using extensive simulations and we demonstrate its applicability on a real-world dataset arising in road traffic modelling.

Learn more

Detecting structural change in dynamic network data has wide-ranging applications. Existing approaches typically divide the data into time bins, extract network features within each bin, and then compare these features over time. This introduces an inherent tradeoff between temporal resolution and the statistical stability of the extracted features. Despite this tradeoff, reminiscent of time-frequency tradeoffs in signal processing, most methods rely on a fixed temporal resolution. Choosing an appropriate resolution parameter is typically difficult and can be especially problematic in domains like cybersecurity, where anomalous behavior may emerge at multiple time scales. We address this challenge by proposing ANIE (Adaptive Network Intensity Estimation), a multi-resolution framework designed to automatically identify the time scales at which network structure evolves, enabling the joint detection of both rapid and gradual changes. Modeling interactions as Poisson processes, our method proceeds in two steps: (1) estimating a low-dimensional subspace of node behavior, and (2) deriving a set of novel empirical affinity coefficients that quantify change in interaction intensity between latent factors and support statistical testing for structural change across time scales. We provide theoretical guarantees for subspace estimation and the asymptotic behavior of the affinity coefficients, enabling model-based change detection. Experiments on synthetic networks show that ANIE adapts to the appropriate time resolution and is able to capture sharp structural changes while remaining robust to noise. Furthermore, applications to real-world data showcase the practical benefits of ANIE's multiresolution approach to detecting structural change over fixed resolution methods.

Learn more

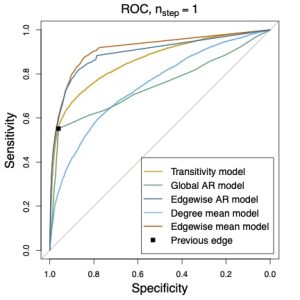
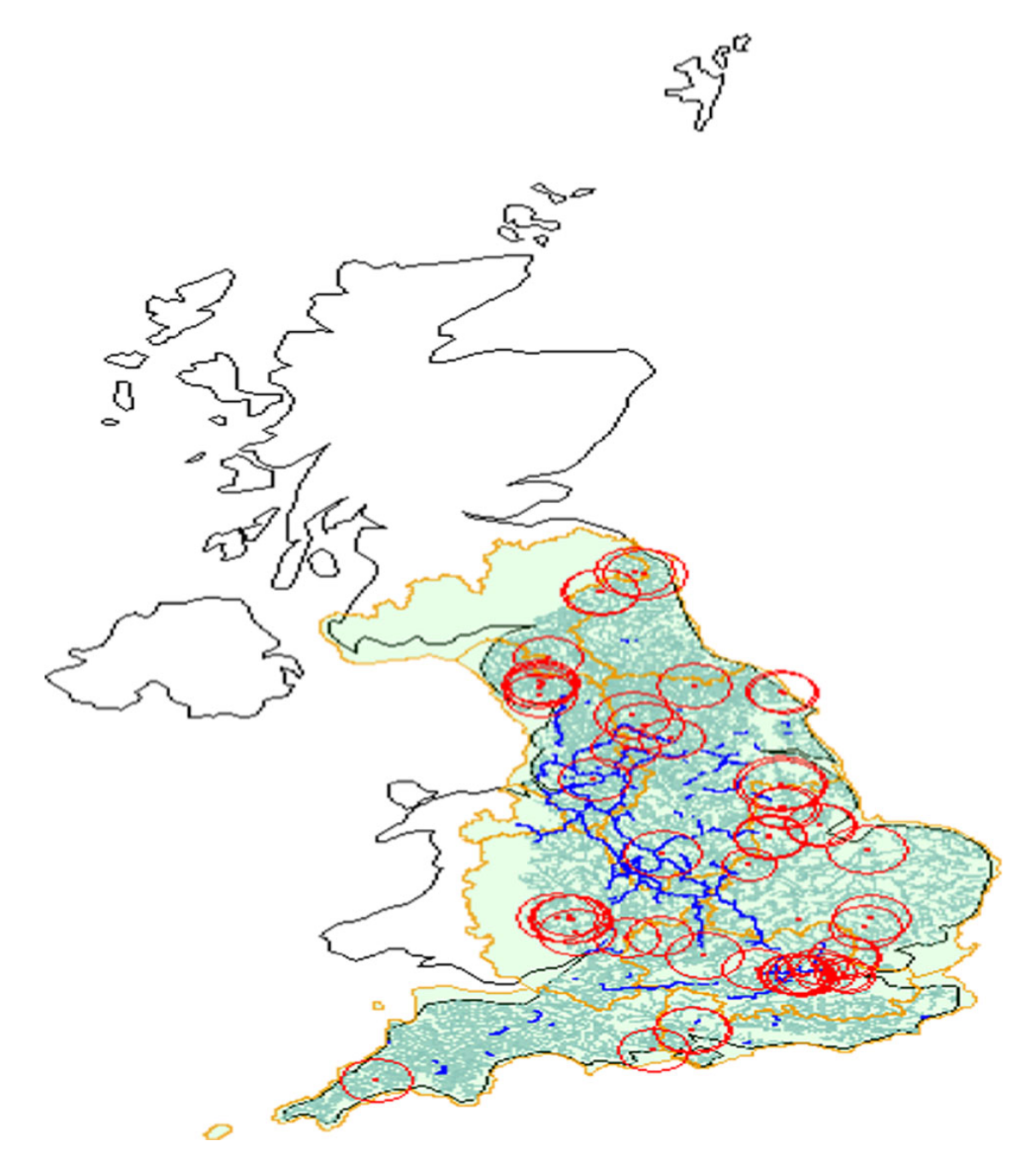
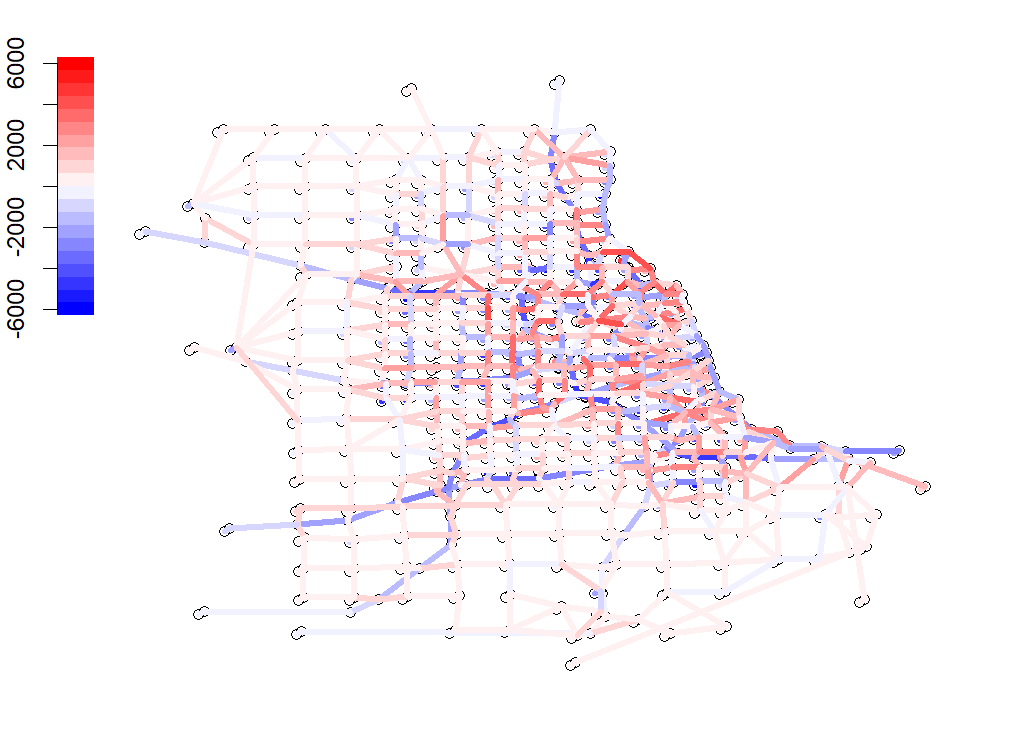
We propose an autoregressive framework for modelling dynamic networks with de- pendent edges. It encompasses models that accommodate, for example, transitivity, degree heterogenenity, and other stylized features often observed in real network data. By assuming the edges of networks at each time are independent conditionally on their lagged values, the models, which exhibit a close connection with temporal ERGMs, facilitate both simulation and the maximum likelihood estimation in a straightforward manner. Due to the possibly large number of parameters in the models, the natural MLEs may suffer from slow convergence rates. An improved estimator for each compo- nent parameter is proposed based on an iteration employing projection, which mitigates the impact of the other parameters (Chang et al., 2021; Chang et al., 2023). Lever- aging a martingale difference structure, the asymptotic distribution of the improved estimator is derived without the assumption of stationarity. The limiting distribution is not normal in general, although it reduces to normal when the underlying process satisfies some mixing conditions. Illustration with a transitivity model was carried out in both simulation and a real network data set.

Learn more